BOJ 2225번 : 합분해 본문

N과 K가 주어졌을때, 0~N의 자연수를 중복선택 포함하여 K개 선택후, 합이 N이 되는 경우의 수를 구하는 문제이다. 즉,
N = 2, K = 3 일 경우에는
(0,0,2), (0,1,1), (0,2,0), (1,0,1), (1,1,0), (2,0,0) 총 6개가 가능하다.
규칙을 찾기 위해 먼저 1개 선택시 부터 3개 선택시 N을 만들기 위한 경우의 수를 계산 해 보았으나, 3개 선택시 부터는 등차수열의 합에 대한 공식 들이 튀어나오면서... 수학같은 문제가 될 뻔 했으나, 컴퓨터 답게 푸는 방법은 아닌것 같아 패스....
좀더 생각해 보니, N = 2, K = 2 일때, (0,2) 는
-
N=0, K=1 일때
-
N=2, K=1 일때
각 경우의 수의 곱과 같다. 즉, 앞의 계산값에 영향을 받는다.. 흠... 너도 dp구나?
그렇다면, N과 K에 대해 표를 그려보자.
0~N 에서 K개를 선택 할때 N을 만들수 있는 경우의 수를 표에 표현하면
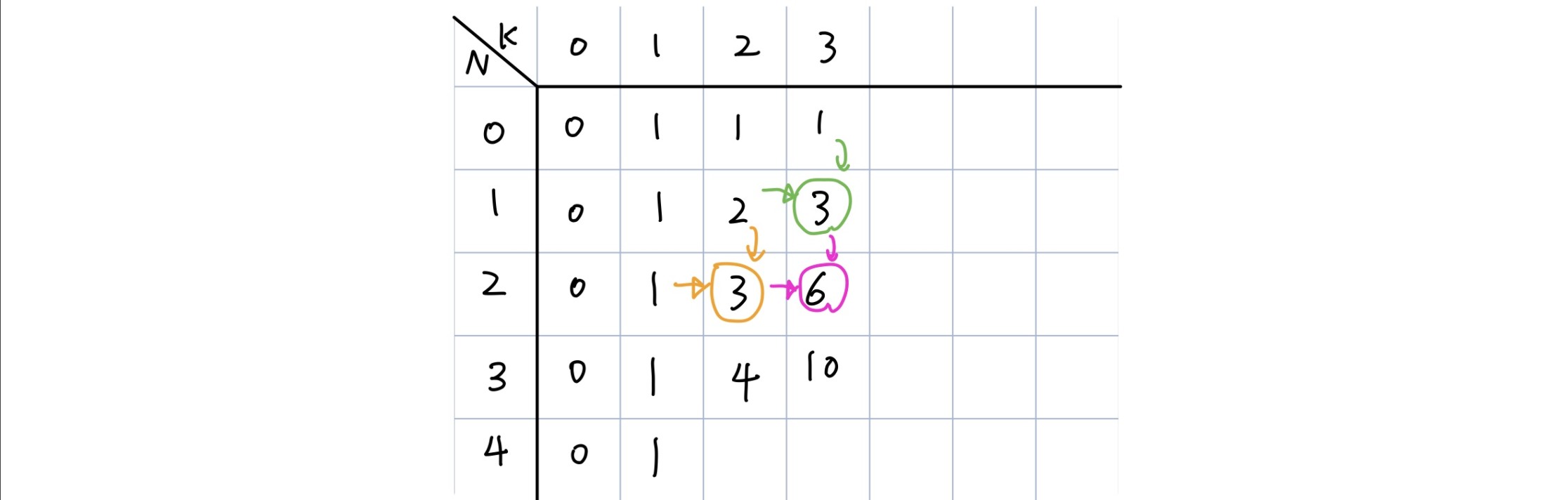
이렇게 규칙이 쏙쏙 보이게 된다.
K=0일때와 N=0 일때를 초기값으로 설정 후, 점화식을 설정하면, 아래와 같이 식을 구성할 수 있다.
dp[n][k] = dp[n-1][k]+dp[n][k-1]
<소스코드>
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
#include<iostream>
using namespace std;
int main() {
int dp[203][203] = { 0, };
int n, k = 0;
cin >> n >> k;
for (int i = 1; i < k + 1; i++)
dp[0][i] = 1;
for (int i = 1; i < k + 1; i++) {
for (int j = 1; j < n + 1; j++) {
dp[j][i] = (dp[j - 1][i] + dp[j][i - 1])%1000000000;
}
}
cout << dp[n][k];
}
http://colorscripter.com/info#e" target="_blank" style="color:#e5e5e5text-decoration:none">Colored by Color Scripter
|
문제 :
https://www.acmicpc.net/problem/2225
2225번: 합분해
첫째 줄에 답을 1,000,000,000으로 나눈 나머지를 출력한다.
www.acmicpc.net
'BOJ' 카테고리의 다른 글
| BOJ 1002번 : 터렛 (0) | 2020.03.15 |
|---|---|
| BOJ 1076번 : 저항 (0) | 2020.03.15 |
| BOJ 9251번 : LCS (0) | 2020.03.15 |
| BOJ 2565번 : 전깃줄 (0) | 2020.03.15 |
| BOJ 1932번 : 정수 삼각형 (0) | 2020.03.15 |
Comments



